Теория межтоновых отношений и кластерная техника Генри Кауэлла (по книге «New Musical Resources»)
2 ноября 2008 / Musica theorica 13
Страницы: 1 2
 Генри Кауэлла называли отцом американской музыки. На протяжении всей своей жизни он не переставал сочинять в самых различных жанрах, проявляя себя как эксперименталист и изобретатель, усиленно занимался педагогической деятельностью. Его вклад в развитие и пропаганду композиторов не только прошлого, но и настоящего огромен.
Генри Кауэлла называли отцом американской музыки. На протяжении всей своей жизни он не переставал сочинять в самых различных жанрах, проявляя себя как эксперименталист и изобретатель, усиленно занимался педагогической деятельностью. Его вклад в развитие и пропаганду композиторов не только прошлого, но и настоящего огромен.
Кауэлл интенсивно применял в сфере композиторского мастерства собственные идеи, изложенные им в разного рода теоретических трудах и, в первую очередь, в наиболее обширном из них — книге «Новые ресурсы музыки», начатой в 1919 году и опубликованной в 1930-м после ряда серьезных доработок. В этом труде Кауэлл знакомит читателя с собственной теорией, построенной на анализе взаимоотношений обертонов. Основополагающий принцип подачи материала — это объяснение многих аспектов с точки зрения обертонового ряда. Новаторские мысли композитора в сфере ритмической организации музыки, техники кластеров и — как прямо вытекающей из этого — специальной нотации, в то время имели довольно широкий резонанс.
В книге Кауэлла три части: «Комбинации тонов», «Ритм», «Образование аккорда». В конце прилагается краткий терминологический словарь. Далее при цитировании книги Кауэлла указывается номер страницы по английскому оригиналу, указанному в сноске1.
Первую часть Кауэлл начинает с описания образования обертонов и предлагает все это выстроить в строго выверенную диаграмму математических вычислений. Таблица Кауэлла в переводе на русский язык помещена ниже. Первая колонка представляет собой до-мажорную гамму. Вторая — обертоны, совпадающие со звуками этого мажорного лада. В третьей даны названия образующихся интервалов. В четвертой — скорость колебания тонов. В пятой — номер обертонов.
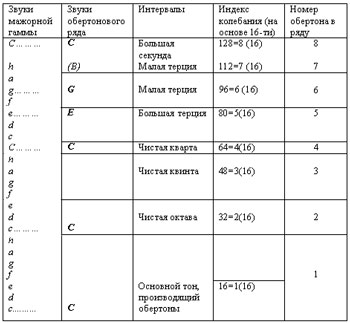 Можно заметить, что скорость колебания вычисляется довольно простой математической комбинацией умножения порядкового номера обертона на 16. Например, шестой обертон = 6 × 16. При этом скорость колебания между обертонами повышается в арифметической прогрессии, а между октавными повторениями основного тона до — в геометрической. Из этого следует, что качество сонантности аккордов прямо вытекает из структуры обертонового ряда. Комбинации тонов из более высоких членов обертонового ряда добавляют диссонантности в комплекс. Это — влияние скорости колебаний звуковых волн, низкая частотность которых соответствует чистому, консонантному звучанию.
Можно заметить, что скорость колебания вычисляется довольно простой математической комбинацией умножения порядкового номера обертона на 16. Например, шестой обертон = 6 × 16. При этом скорость колебания между обертонами повышается в арифметической прогрессии, а между октавными повторениями основного тона до — в геометрической. Из этого следует, что качество сонантности аккордов прямо вытекает из структуры обертонового ряда. Комбинации тонов из более высоких членов обертонового ряда добавляют диссонантности в комплекс. Это — влияние скорости колебаний звуковых волн, низкая частотность которых соответствует чистому, консонантному звучанию.
Кроме подразделения характера звучания на консонансы и диссонансы Кауэлл использует термин дискорд. Звуковой материал дискорда сформирован, как пишет Кауэлл, «высокими обертоновыми соотношениями, где тоны диссонантных аккордов распределены так, что возможность их восприятия становится весьма сложной» (Р. 10). Можно понять из цитаты, что дискорд представляет собой «супердиссонантные» комбинации, довольно сложно дифференцируемые слухом. К этому, возможно, следует прибавить фактор количества тонов, который усиливает высокую сонантность дискорда. Принцип разделения или рассредотачивания дистóнов2 в музыкальном пространстве является одним из показателей дискорда. Но, точные границы дис/кон-сонансов и дискорда в ряду обертонов автором книги не указаны, так как для их определения основополагающую роль играет слушательский опыт. «Этот факт, доказанный историей музыкального прогресса, в соединении с акустическим фактом говорит, что нет никакого смысла показывать произвольные различия между ними, а также устанавливает относительность консонансов, диссонансов и дискорда» (Р. 11).
Сравним две пары интервалов. Первая: интервалы e-g (терция) и c-b (септима) и вторая: интервалы e-g и g-e (секста). Различий между интервалами первой пары не больше, чем между интервалами второй пары, хотя и интервалы второй пары определенно трактуются как консонансы. Конечно, интервал септимы не является сильным диссонансом с точки зрения обертонового ряда и многих композиторов прошлого и нынешнего века, но, как пишет Кауэлл, «принятая ранее диссонантность интервала 4:7, т.е. с-b, вполне оправдана акустическими законами скорости колебания, а также слушательским ощущением» (Р.11-12). Кауэлл описывает «эволюцию принятия» тех или иных интервалов с самых древних времен.
Конечно же, стоит сказать о том, что именно в этой работе Кауэлла впервые в музыкальной науке появляется термин полигармония. Раздел, посвященный этой теме, автор начинает с объяснения акустических законов обертонов, которые исходят не только от фундаментального тона, но также от самих обертонов. Таким образом, если одновременно сыграть, например, трезвучия от с и g, то здесь будет действовать математический закон обертоновых соотношений. Данный аккорд сформирован из двух малых групп (группа g и группа c), которые во многом зависят от качества их собственного основного тона. Характерное качество такого тона может объясняться степенью приближенности к первоначальному фундаментальному тону или, что тоже возможно, динамическими свойствами. Полное единство (или одновременное взятие) таких малых групп и называется Кауэллом полиаккордом. Он, фактически, образован из фундаментального тона, так как именно он представляет первооснову всех малых групп. «При применении полигармонии и последовательности полиаккордов имеет смысл способ „упрощения“ (simplification). Поскольку, если единые гармонии непрерывно строятся вверх с помощью использования все большего количества тонов, они становятся чрезмерно сложными; но если эти тоны упрощены группировкой в пределах гармонии в соотносящиеся друг с другом единства (related units), становится возможным сохранять простоту и ясность в использовании многих различных тонов вместе» (P. 25-26). Такие «единства» в теории гармонии принято называть субаккордами, то есть аккордами, представляющими собой часть какого-либо целого комплекса. Кауэлл, однако, этого термина не использует.
Самым простым видом будет полиаккорд, построенный из аккордов кварто-квинтового соотношения. Построение полиаккорда по трезвучиям, находящимся в терцовом или в секундовом соотношении является по степени сложности следующим этапом организации полигармонического материала.
Полиаккорды могут быть также построены из звуков обертонового ряда. В таком принципе построения можно заметить одну логическую линию, не обозначенную Кауэллом3. А именно — этапы интервальных соотношений аккордов внутри полиаккордов (от простого к более сложному) соответствуют интервальному строению обертонового ряда. Таким образом, обертоновый ряд можно разделить на несколько отделов. Первый отдел, который будет соответствовать начальному (кварто-квинтовому) этапу построения «внутренних» аккордов, состоит из первых четырех обертонов, включающих октаву, квинту и кварту. Второй, соответствующий следующему этапу, включает в себя с пятого по седьмой обертоны, то есть терции. Секундовый отдел следует такой же идее. Нужно отметить, что аналогичный принцип, основывающийся на последовательных интервальных стадиях в обертоновом ряду, будет рассмотрен Кауэллом в последней части книги в разделе о кластерах. При этом субаккорды внутри должны быть разделены, «то есть не должны накладываться и перепутываться друг с другом; иначе эффект полиаккорда „сходит на нет“, и звучит единый диссонанс (single dissonance)» (Р.26).
Полиаккорды могут быть также построены из звуков обертонового ряда. Кроме обертонов материалом для различных комбинаций могут служить унтертоны4 (undertones), то есть минорные трезвучия. В разговоре об унтертонах Кауэлл отмечает тот факт, что в минорном трезвучии основной тон находится вверху, потому что именно он производит ряд унтертонов. Но, так как уже довольно основательно закрепились известные нам названия минорных трезвучий (от нижнего тона), Кауэлл не считает нужным вводить новые.
При той или иной последовательности полиаккордов можно использовать привычные нам неаккордовые звуки. Те же самые проходящие и вспомогательные звуки выполняют функцию украшения музыкального материала. В этом случае Кауэлл применяет термины ровный (plain) и украшенный (embellishment). Если за единицу в данном случае мы возьмем не звук, а аккорд, то получим такой же спектр различных преобразований. Соединяя аккорды в контрапункт, Кауэлл пишет о том, что все те способы, связанные с «ровными» и «украшенными» линиями могут быть применены и в аккордах. Соответственно, такой вид полигармонического развития он называет контраккордом (counter-chord) или аккордом против аккорда (chord against chord). Здесь единицей контрапунктического материала является не один звук, а целый аккорд. При этом структура аккорда в дальнейших проведениях изменена. И это вполне объяснимо, так как связующим звеном здесь является последовательность фундаментальных тонов. Измененная структура аккорда никак не влияет на фундаментальный тон. Таким образом, контрапункт проводится немного на ином уровне, чем обычно. Главным звукообразующим фактором здесь является неизменная последовательность фундаментальных тонов, строго выдержанная во всех аккордо-голосах. Кауэлл приводит собственные примеры, где ясно показывает контраккордовую технику.
 Третий параграф посвящен проблеме звукового качества (Tone-quality) и здесь многие аспекты Кауэлл объясняет при помощи техник игры на деревянных духовых инструментах. Для того чтобы прояснить многие ценные мысли Кауэлла, мы обратились к кларнетисту О. И. Танцову, владеющему техникой, которая будет изложена ниже.
Третий параграф посвящен проблеме звукового качества (Tone-quality) и здесь многие аспекты Кауэлл объясняет при помощи техник игры на деревянных духовых инструментах. Для того чтобы прояснить многие ценные мысли Кауэлла, мы обратились к кларнетисту О. И. Танцову, владеющему техникой, которая будет изложена ниже.
Весь этот параграф книги представляет собой краткое изложение основных понятий без каких-либо разъяснений (1,5 страницы) и потому почти весь материал останется непонятым читателями. Далее в нашей работе даются не только разъяснения материалов Кауэлла, но и изложение дополнительных технических приемов игры.
Любой взятый на деревянных духовых инструментах звук при помощи разных аппликатурных положений может звучать по-разному, то есть иметь различное звуковое качество, которое зависит от того, какой частичный тон в данном звуке преобладает. «В звуке флейты частичные тоны, получающие четные номера, более выпуклы, при этом частичные тоны, получающие четные номера слабее, в то время как на кларнете все с точностью наоборот» (P. 32). Поясним эту мысль Кауэлла.
Как у флейты, так и у кларнета каждый звук имеет ряд обертонов; некоторые из них более или менее выделяются. Если обертоновый ряд представить в виде цифровой вертикали, где отсчет будет начинаться от фундаментального тона, то наиболее яркими в звуке флейты будут четные обертоны, а кларнета — нечетные. Каждый звук берется с преобладанием того или иного возможного частичного тона — более низкого или наоборот, более высокого в ряду обертонов. При этом фундаментальный тон остается звучать, то есть обертоновый звук накладывается на звучание. В результате мы слышим два звука, один из которых является фундаментальным, другой — его обертоном. Выбор этих обертонов, как уже было сказано выше, во многом зависит от инструмента. Каждый взятый таким образом обертон несет в себе свою собственную характеристику, выражаемую в звучании. Таким образом, от выбранного обертона зависит та или иная степень качества звука. В этом случае, определенный обертон является неким «спутником» звука, перемена которого оборачивается переменой в качестве звучания, при неизменном звуке. В этом случае происходит эффект расщепления. Такое «рассечение» (разбивание) на два субтона5 получило свое название — sons fendus (от франц. «рассекать», «разбивать»). Так называемый «расщепленный звук» предполагает наличие основного и производного звука.
Таким образом, мы видим, что на деревянных духовых инструментах (у Кауэлла это флейта и кларнет) мы можем взять не только отдельный обертон (без фундаментального тона), но и основной звук с одновременно взятым его частичным тоном.
Кауэлл пишет: «Результат игры на флейте и кларнете одновременно является почти совершенным отражением обертонового ряда, и поэтому мы получаем богатое звуковое качество» (P. 32). Попробуем это объяснить.
В тоне флейты более рельефны и выпуклы те обертоны, которые у кларнета выделяются в наименьшей степени. К примеру, если сыграть одновременно на флейте и на кларнете звук с первой октавы и при этом «звуковыми спутниками» у этих инструментов будут самые близкие возможные обертоны (у флейты — с второй октавы, то есть четный — второй — обертон, у кларнета — g второй октавы, то есть нечетный — третий — обертон), то мы получаем точную проекцию обертонового ряда. В целом получается три звучащих одновременно звука на обоих инструментах — c первой октавы, c второй октавы и g второй октавы. Это то, что Кауэлл называет «ясным», чистым звучанием, которое продиктовано степенью приближенности обертона к взятому звуку.
- Сowell H. New musical resources. New York, 1930. [обратно]
- Дистóн, по сути, является одним из составляющих диссонантных групп. Этот термин используется в данной работе для того, чтобы «разгрузить» смысл термина диссонанс, так как последний представлен в вертикали (консонанс — диссонанс — дискорд). [обратно]
- Возможно, данное обоснование и имелось ввиду Кауэллом, так как интервальное строение обертонового ряда является здесь основополагающим. Тем более, что данный прием разделения на части обертонового ряда по принципу «интервальной связности» (интервалы каждой части изложены последовательно и родственны по структуре) будет применяться в других главах книги. [обратно]
- Этот термин, как известно, фигурирует в работе Г. Римана «Упрощенная гармония» (Riemann H. Vereinfachte Harmonielehre oder die Lehre von den tonalen Funktionen der Akkorde. London, N.-Y., 1893. Английский перевод вышел в 1895 году). К сожалению, мы не знаем точно, был ли Кауэлл знаком с этой книгой. Но использование этого термина в данном труде свидетельствует о его бытовании в американской практике. [обратно]
- Здесь термин «субтон» следует понимать как составляющий элемент определенной звуковой структуры, в данном случае — как часть «расщепленного звука». [обратно]
Страницы: 1 2